Question

A dumbbell-shaped object is composed by two equal masses, m, connected by a rod of negligible mass and length r. If I_1 is the moment of inertia of this object with respect to an axis passing through the center of the rod and perpendicular to it and l_2 is the moment of inertia with respect to an axis passing through one of the masses, it follows that:a. I1=I2b. I1>I2c. I2>I1

Answer 1

I2>I1

Step-by-step explanation:

This problem can be solved by using the parallel axis theorem. If the axis of rotation of a rigid body (with moment of inertia I1 at its center of mass) is changed, then, the new moment of inertia is gven by:

`I_2=I_(1)+Md^2`

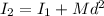
where M is the mass of the object and d is the distance of the new axis to the axis of the center of mass.

It is clear that I2 is greater than I1 by the contribution of the term Md^2.

I2>I1

hope this helps!!