Answer:
(a) The Normal Distribution,
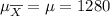 , and standard deviation of
, and standard deviation of
 hours. (b) The 90% confidence interval of the true mean lifetime goes from 1257.04 to 1302.96 hours. hours.
hours. (b) The 90% confidence interval of the true mean lifetime goes from 1257.04 to 1302.96 hours. hours.
Step-by-step explanation:
We want to estimate the true value of the mean for a population taking a sample from this population. When the sample is greater or equal to 30
 , no matter which distribution the data come from, the distribution of the sample means will have a normal distribution with mean
, no matter which distribution the data come from, the distribution of the sample means will have a normal distribution with mean
 (the mean of the population) and a standard deviation of
(the mean of the population) and a standard deviation of
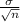 . Mathematically:
. Mathematically:
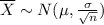
Likewise, the variable Z will behave as normal standard distribution
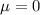 and
and
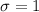 .
.
Then
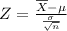
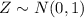
Key aspects to solve this question:
- The sample size is n = 100 bulbs.
- The mean
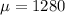 hours.
hours. - The sample standard deviation

Having this information at hand, we are prepared to solve the questions.
The probability distribution of the mean lifetime from the sample of 100 light bulbs
The light bulb lifetimes come from an exponential probability distribution. However, since the sample size in greater than 30, that is,
 , the sampling distribution will follow a normal distribution (as previously explained). Then, the probability distribution of the mean lifetime from the sample of 100 light bulbs is the normal distribution.
, the sampling distribution will follow a normal distribution (as previously explained). Then, the probability distribution of the mean lifetime from the sample of 100 light bulbs is the normal distribution.
In this conditions, the mean and standard deviation of this sample mean lifetime are:
The mean of the sample is the same of the population, i. e.,
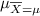 . This is also the mean for the distribution of the sample means. Therefore,
. This is also the mean for the distribution of the sample means. Therefore,
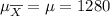 hours.
hours.
The standard deviation in this case is not the population standard deviation (since we do not have this value). Instead, we have the sample standard deviation given
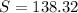 . Thus, the standard deviation for the sample is
. Thus, the standard deviation for the sample is
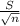
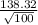
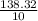
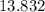 hours.
hours.
The 90% confidence interval of the true mean lifetime
With this interval, we need to find two values. We do not have the value for the population standard deviation. The confidence interval is given by the following formula:
Upper limit =

Lower limit =
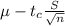
Where
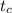 is the confidence coefficient for a t-student distribution, with n - 1 degrees of freedom. For a 90% confidence interval is, approximately,
is the confidence coefficient for a t-student distribution, with n - 1 degrees of freedom. For a 90% confidence interval is, approximately,
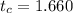 .
.
We have already determined the values for
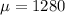 hours and
hours and
 hours. Therefore:
hours. Therefore:
Upper limit =
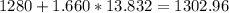 hours.
hours.
Lower limit =
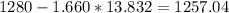 hours.
hours.
Thus, the 90% confidence interval of the true mean lifetime goes from 1257.04 to 1302.96 hours.