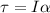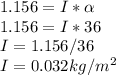Question

A textbook of mass 2.05 kg rests on a frictionless, horizontal surface. A cord attached to the book passes over a pulley whose diameter is 0.200 m , to a hanging book with mass 3.05 kg . The system is released from rest, and the books are observed to move a distance 1.30 m over a time interval of 0.850 s .

A. What is the tension in the part of the cord attached to the textbook?
B. What is the tension in the part of the cord attached to the book?
C. What is the moment of inertia of the pulley about its rotation axis?

Answer 1

a) Tension on the textbook, T₁ = 7.38 N

b) Tension on the book, T₂ = 18.94 N

c) Moment of Inertia of the pulley,
`I = 0.032 kg/m^(2)`

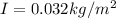
Step-by-step explanation:

Mass of the textbook, m₁ = 2.05 kg

diameter of the pulley, d = 0.2 m

radius of the pulley, r = 0.1 m

The system is released from rest, u = 0 m/s

S = 1.30 m

t = 0.850 s

a) To get the tension, T₁ = m₁a

S = ut + 1/2 at²

1.30 = (0*0.85) + (0.5*a*0.85²)

1.30 = 0.36125a

a = 1.30/0.36125

a = 3.60 m/s

The tension in the part of the cord attached to the textbookwill be:

T₁ = 2.05 * 3.60

T₁ = 7.38 N

b) Tension in the part of the book

The mass of the book, m₂ = 3.05 kg

Since the book is hanging, the tension applied to it is acting upwards while the weight is acting downwards.

For an upward tension:

Therefore, m₂g -T₂ = m₂a

(3.05*9.81) -T₂ = (3.05*3.60)

T₂ = 29.92 - 10.98

T₂ = 18.94 N

c) moment of inertia of the pulley about its rotation axis

The torque acting on the pulley can be given by the equation:

`\tau = (T_(2) - T_(1) )r\\\tau = (18.94 -7.38) * 0.1\\\tau = 1.156 Nm`

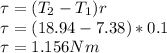
Angular acceleration of the pulley, α = a/r

α = 3.60/0.1

α = 36 rad/s²

The torque acting on the pulley,
`\tau = I \alpha`

`1.156= I * \alpha\\1.156 = I * 36\\I = 1.156/36\\I = 0.032 kg/m^(2)`

Answer 2

a. 7.38 N b. 40.87 N c. 0.113 kg-m²

Step-by-step explanation:

a. Let T be the tension in the cord. For the textbook, T = ma since no other force acts on it and it is an horizontal force, and m = mass = 2.05 kg and a = acceleration. We find the acceleration from s = ut + 1/2at² where u = initial speed = 0 (since it starts from rest), s = distance moved = 1.30 m and t = time = 0.850 s.

Substituting these values into s,

1.30 m = 0 × 0.850 + 1/2a × 0.850² = 0 + 0.36125a

1.30 = 0.36125a

a = 1.30/0.36125 = 3.6 m/s²

Substituting this into T, we have

T = ma = 2.05 kg × 3.6 m/s² = 7.38 N

b. Let T be the tension in the cord attached to the book. The book has the only vertical forces acting on it as the tension, T(acting upwards) and its weight mg (acting downwards). So the net force acting on it is

T - mg = ma

T = m(a + g)

substituting a = 3.6 m/s² and g = 9.8 m/s² and m = 3.05 kg

T = 3.05(3.6 + 9.8) = 3.05 × 13.4 = 40.87 N

c. Since the tangential acceleration of the pulley is also the acceleration of the masses, the a = rα where r = radius of pulley = 0.200 m/2 = 0.100 m and α = angular acceleration of the pulley.

α = a/r = 3.6 m/s² ÷ 0.100 m = 36 rad/s²

Now, the torque on the pulley τ = Tr = Iα where I = moment of inertia of pulley about its rotational axis and T = tension in cord attached to book and r = radius of pulley = 0.200 m/2 = 0.100 m

From the equation above, I = Tr/α

Substituting the variables we have

I = 40.87 N × 0.100 m ÷ 36 rad/s² = 0.113 kg-m²