Question

Expand (5 + z)4

choices are:

625 + 500z + 150z2 + 20z3 + z4

625 + 375z + 150z2 + 15z3 + z4

625 + 250z + 100z2 + 10z3 + z4

625 + 125z + 25z2 + 5z3 + z4

Answer 1

Option 1

625 + 500z + 150z² + 20z³ + z⁴

Explanation:

(5 + z)⁴

4C0×5⁰×z⁴ + 4C1×5¹×z³ + 4C2×5²×z² + 4C3×5³×z¹ + 4C4×5⁴×z⁰

z⁴ + 20z³ + 150z² + 500z + 625

Answer 2

A

Explanation:

We want to expand:
`(5 + z)^4`. We need to use the Binomial Theorem for this, which states that for a monic expression like x + k (where k is a constant) to the nth power, the coefficients of the terms will follow the terms in the nth row of the Pascal Triangle. These terms in the Pascal Triangle are of the form:

nC0 , nC1 , nC2 , .... , nC(n - 1) , nCn ---- here, nCk is combinations:
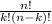`(n!)/(k!(n-k)!)` , where ! denotes factorial

So, since the power here is 4, we will be using: 4C0, 4C1, 4C2, 4C3, and 4C4 as our coefficients of the terms.

Let's make 5 + z into z + 5. Now, we expand:

`(z+5)^4=4C0 * z^4+4C1*z^3*5+4C2*z^2*5^2+4C3*z*5^3+4C4*5^4`

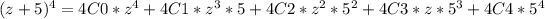
4C0 = 1 , 4C1 = 4 , 4C2 = 6 , 4C3 = 4 , and 4C4 = 1:

`1 * z^4+4*z^3*5+6*z^2*5^2+4*z*5^3+1*5^4=z^4+20z^3+150z^2+500z+625`

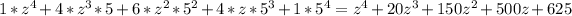
Thus, the answer is A.

Hope this helps!