Question

A small resort is situated on an island that lies exactly 3 miles from P, the nearest point to the island along a perfectly straight shoreline. 10 miles down the shoreline from P is the closest source of fresh water. If it costs 2.3 times as much money to lay pipe in the water as it does on land, how far down the shoreline from P should the pipe from the island reach land in order to minimize the total construction costs?

Answer 1

The distance from the shoreline from P the pipe from the island will reach land in order to minimize the total construction cost is 0 m, or the pipe should be routed to the point P

Explanation:

We note that, cost to lay pipe in water = 2.3 × cost to lay pipe on land

Distance of the small resort on the island from point p on the shoreline = 3 miles

Location of the closest source of fresh water is 10 miles along the shoreline from p

∴ The small resort, the point p and the closest source of the fresh water on the shoreline together form a right triangle with sides

Height = 3 miles

Base = 10 miles and

Hypotenuse =
`√(3^2 + 10 ^2) = √(109) = 10.44 \, m`

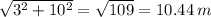
To find the cost of laying the pipeline by the various route, we multiply the water routes by 2.3 and the land routes by 1 and we get

Costs:

Height = Water route = 2.3 × 3 miles = 6.9

Base = Land route = 1 × 10 miles = 10

Hypotenuse = Water route = 2.3 × 10.44 miles = 24.012

Therefore, the two routes are either

10 miles to point p and 3 miles across the water to the resort with a cost = 10 + 6.9 = 16.9 or

Directly to the small resort through 10.44 miles across the water with cost = 24.012

Therefore, to minimize cost, the pipe should come from the resort to P from there to the fresh water source.

That is the distance from the shoreline from P the pipe from the island will reach land in order to minimize the total construction cost = 0 m.