The other answer is just wrong.
There are 9•9•8 = 648 distinct 3-digit codes. The first digit can be any numeral from 1-9, the next digit can be any from 0-9 minus the one used in the first position, and the last digit can be any from 0-9 minus both the numerals used in the first two positions.
But that doesn't even account for the divisibility constraint.
Let the code be
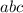 . We can expand this as
. We can expand this as
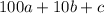
In order for this to be divisible by 4, we observe that
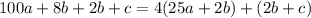
so we only need
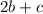 to be divisible by 4.
to be divisible by 4.
The last digit must be even, so there are only 5 choices for the last digit. I list the possibilities and outcomes below. For some integer
 , we need
, we need
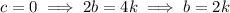
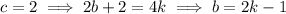
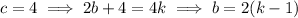
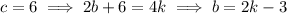
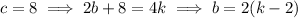
Ignoring
 for the moment, in the cases of
for the moment, in the cases of
 ,
,
 is also even. This leaves 3 choices for
is also even. This leaves 3 choices for
 and 2 choices for
and 2 choices for
 .
.
Likewise, in the cases of
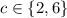 ,
,
 is odd. This leaves 2 choices for
is odd. This leaves 2 choices for
 and 5 choices for
and 5 choices for
 .
.
Now taking into account the choice for
 , we have the following decision tree.
, we have the following decision tree.
• If
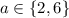 and
and
 , then
, then
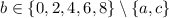 - a total of 2•3•3 = 18 codes.
- a total of 2•3•3 = 18 codes.
• If
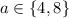 and
and
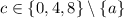 , then
, then
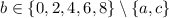 - a total of 2•2•3 = 12 codes.
- a total of 2•2•3 = 12 codes.
• If
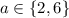 and
and
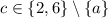 , then
, then
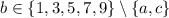 - a total of 2•1•5 = 10 codes.
- a total of 2•1•5 = 10 codes.
• If
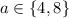 and
and
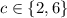 , then
, then
 - a total of 2•2•5 = 20 codes.
- a total of 2•2•5 = 20 codes.
• If
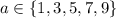 and
and
 , then
, then
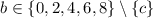 - a total of 5•3•4 = 60 codes.
- a total of 5•3•4 = 60 codes.
• If
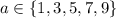 and
and
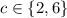 , then
, then
 - a total of 5•2•4 = 40 codes.
- a total of 5•2•4 = 40 codes.
Hence there are a total of 18 + 12 + 10 + 20 + 60 + 40 = 160 codes.