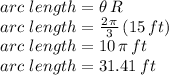Question

A carousel horse travels on a circular path with a radius of 15 ft. How many feet does the horse travel over an angle of 2π3 radians? Round to the nearest foot.

2π3 radians = ft

Answer 1

`arc\,\,length=10\,\pi\,ft\\arc\,\,length=31.41\,ft`

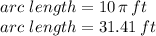
Explanation:

Recall that the formula for the length of an arc of circumference is given by the formula:

`arc\,\,length=\theta\,R`

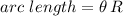
where
`\theta` is the radian form of central angle subtended , and R is the radius of the circumference. What is important is to have the angle given in radians for this formula to be valid.

In our case, the angle (
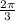`(2\pi)/(3)` ) is already in radians, so we can apply the formula directly:

`arc\,\,length=\theta\,R\\arc\,\,length=(2\,\pi)/(3) \,(15\,ft)\\arc\,\,length=10\,\pi\,ft\\arc\,\,length=31.41\,ft`