Question

A study was conducted to determine the proportion of people who dream in black and white instead of color. Among 317 people over the age of 55. 70 dream in black and white, and among 296 people under the age of 25. 12 dream in black and white.

Use a 0.01 significance level to test the claim that the proportion of people over 55 who dream in black and white is greater than the proportion for those under

a. Test the claim using a hypothesis test.

b. Consider the first sample to be the sample of people over the age of 55 and the second sample to be the sample of people under the age of 25. What are the null and alternative hypotheses for the hypothesis test?

Answer 1

Explanation:

Hello!

The objective is to compare if the proportion of people over 55 years old that dream in black and white is greater than the proportion of those under the age fo 25 that dream in black and white.

To do the comparison two random samples where taken:

Sample 1:

X₁: Number of people over the age of 55 that dream in black and white of a sample of 317.

n₁= 317

x₁= 70

p₁'= x₁/n₁= 70/317= 0.22

Sample 2

X₂: Number of people under the age of 25 that dream in black and white of a sample of 296

n₂= 296

x₂= 12

p₂'= x₂/n₂= 12/296= 0.04

Pooled sample proportion:
`p'= (x_1+x_2)/(n_1+n_2)= (70+12)/(317+296) = 0.13`

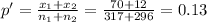
a.

The parameters of interest are the population proportions p₁ and p₂, the claim is that the proportion of people over 55 that dream in black and white is greater than than the proportion of people under 25 that dream in black and white, symbolically: p₁ > p₂

H₀: p₁ ≤ p₂

H₁: p₁ > p₂

α: 0.01

The statistic for this test is the approximation of the standard normal distribution:

`Z= \frac{(p'_1-p'_2)-(p_1-p_2)}{\sqrt{p'(1-p')(1)/(n_1) +(1)/(n_2) } }`≈N(0;1)

`Z_(H_0)= \frac{(0.22-0.04)-0}{\sqrt{0.13(1-0.13)*[(1)/(317) +(1)/(296) ]} } = 6.62`

The p-value of this test is one-tailed to the right, just as it is the test.

p-value < .00001

The decision rule for the p-value approach is:

If the p-value ≤ α, the decision is to reject the null hypothesis.

If the p-value > α, the decision is to not reject the null hypothesis.

In this case, the decision is to reject the null hypothesis.

Using a level of significance of 1%, there is significant evidence to reject the null hypothesis. Then you can conclude that the population proportion of people over the age of 55 that dreams in black and white is greater than the population of people under the age of 25 that dreams in black and white.

I hope this helps!