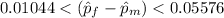Question

Recall the survey you took during the first week of class. One of the questions was “do you agree that it is inappropriate to speak on a cellphone while at a restaurant?” Of the 1913 females that responded to the survey, 1729 agreed with this statement. Of the 1276 males that responded to this survey, 1111 agreed with this statement. Test to see if there is any difference between males and females with respect to how they feel about this issue. Use a significance level of .05.

State the appropriate null and alternative hypotheses.


Calculate the test statistic and report the p-value.

State your conclusion in context of the problem.

Based only on the results of the hypothesis test, would you expect a 95% confidence interval to include 0? Explain.

Calculate and interpret a 95% confidence interval for the difference between males and females.

Answer 1

`a) \ H_o:\hat p_f=\hat p_m\\\ \ \ H_a:\hat p_f\\eq \hat p_m\\\\b) z\ test=2.925, \ p\ value(two-tail)=0.003444\\\\\\`

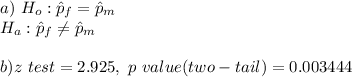
c) Reject H_o since there is sufficient evidence to suggest that there is difference between males and females with respect to how they feel about this issue.

d. No. Interval does not include zero

e.
`CI=[0.01044<(\hat p_f-\hat p_m)<0.05576`

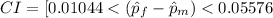
We are 95% confident that the proportional difference lies between the [0.010444,0.05576] interval.

Explanation:

a. The null hypothesis is that there is no difference between males and females with respect to how they feel about this issue:

`H_o:p_m=p_f`

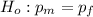
-The alternative hypothesis is that there is some difference between males and females with respect to how they feel about this issue:

`H_a:p_m\\eq p_f`

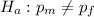
where
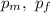`p_m, \ p_f` is the proportion of males and females respectively.

b. The proportion of males and females in the study can be calculated as follows:

`\hat p=(x)/(n)\\\\\hat p_f=(1729)/(1913)=0.9038\\\\\hat p_m=(1111)/(1276)=0.8707`

`\hat p=(x_f+x_m)/(n_m+n_f)=(1111+1729)/(1276+1913)=0.8906`

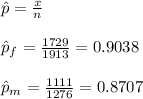
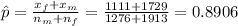
#We then calculate the test statistic using the formula:

`z=\frac{(\hat p_f-\hat p_m)}{\sqrt{\hat p(1-\hat p)((1)/(n_f)+(1)/(n_m))}}\\\\\\=\frac{(0.9038-0.8707)}{\sqrt{(0.8906*0.1094)((1)/(1913)+(1)/(1276))}}\\\\\\=2.9250\\\\\therefore p-value=0.001722\\`

`\# The \ two \ tail \ p-value \ is\\\\=0.01722* 2\\\\=0.003444`

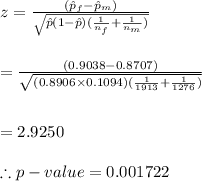
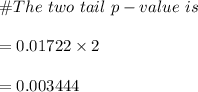
c. Since p<0.05:

`p<0.05\\\\0.00344<0.05\\\\\therefore Reject \ H_o`

Hence, we Reject the Null Hypothesis since there is sufficient evidence to suggest that there is difference between males and females with respect to how they feel about this issue

d. The 95% confidence interval can be calculated as below:

`CI=(p_f-p_m)\pm z_(\alpha/2)\sqrt{(\hat p_m(1-\hat p_m))/(n_m)+(\hat p_f(1-\hat p_f))/(n_f)}\\\\=(0.9038-0.8707)\pm 1.96√(0.00008823+0.000045449)\\\\=0.03310\pm 0.02266\\\\=[0.01044,0.05576]`

Hence, the confidence interval does not include 0

e. The 95% confidence interval calculated from above is :

`0.01044<(p_f-p_m)<0.05576`

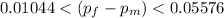
Hence, we are 95% confident that the proportional difference will fall between the interval
`0.01044<(\hat p_f-\hat p_m)<0.05576`