Question

Somebody help me with this

Answer 1

A: 112°

B: 95°

C: 68°

D: 85°

Explanation:

Opposite angles add up to 180

8z + 14z - 7 = 180

22z = 187

z = 8.5

A = 14(8.5) - 7

A = 112

C = 8(8.5)

C = 68

D = 10(8.5)

D = 85

B = 180 - 85

B = 95

Answer 2

Given:

Given that the quadrilateral ABCD is inscribed in the circle.

The measure of ∠A is (14z - 7)°

The measure of ∠C is (8z)°

The measure of ∠D is (10z)°

We need to determine the measures of ∠A, ∠B, ∠C and ∠D

Value of z:

We know the property that the opposite angles of a quadrilateral inscribed in a circle are supplementary.

Thus, we have;

`\angle A+ \angle C=180^(\circ)`

Substituting the values, we have;

`14z-7+8z=180`

`22z-7=180`

`22z=187`

`z=8.5`

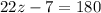
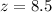
Thus, the value of z is 8.5

Measure of ∠A:

The measure of ∠A can be determined by substituting the value of z.

Thus, we have;

`\angle A=14(8.5)-7`

`\angle A=119-7`

`\angle A=112^(\circ)`

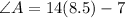
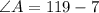
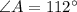
Thus, the measure of ∠A is 112°

Measure of ∠C:

The measure of ∠C can be determined by substituting the value of z.

Thus, we have;

`\angle C=8(8.5)`

`\angle C =68^(\circ)`

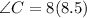
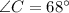
Thus, the measure of ∠C is 68°

Measure of ∠D:

The measure of ∠D can be determined by substituting the value of z.

Thus, we have;

`\angle D=10(8.5)`

`\angle D=85^(\circ)`

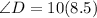
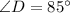
Thus, the measure of ∠D is 85°

Measure of ∠B:

The angles B and D are supplementary.

Thus, we have;

`\angle B+ \angle D=180^(\circ)`

Substituting the values, we get;

`\angle B+ 85^(\circ)=180^(\circ)`

`\angle B=95^(\circ)`

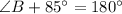
Thus, the measure of ∠B is 95°