Given:
Given that the composite figure is made up of a triangular prism and a pyramid.
The height of the pyramid is 19.5 units.
The length of the prism is 25 units.
The base of the triangle is 22 units.
The height of the triangle is 10 units.
We need to determine the volume of the composite figure.
Volume of the triangular pyramid:
The volume of the triangular pyramid can be determined using the formula,
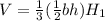
where b is the base of the triangle and h is the height of the triangle and H₁ is the height of the pyramid.
Substituting b = 22 , h = 10 and H₁ = 19.5, we get;
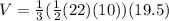
Simplifying, we get;

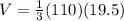
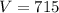
Thus, the volume of the triangular pyramid is 715 cubic units.
Volume of the triangular prism:
The volume of the triangular prism can be determined using the formula,
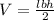
Substituting l = 25, b = 22 and h = 10, we get;
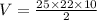
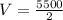
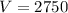
Thus, the volume of the triangular prism is 2750 cubic units.
Volume of the composite figure:
The volume of the composite figure can be determined by adding the volume of triangular prism and triangular pyramid.
Thus, we have;
Volume = Volume of prism + Volume of pyramid.
Substituting the values, we have;
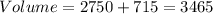
Thus, the volume of the composite figure is 3465 cubic units.
Hence, Option d is the correct answer.