Question

A packaging company wants to fit 6 energy drink cans in a cardboard box, as shown below. The

bottom of each can is a circle with a radius of 4 cm. What is the area of the bottom of the box not
taken up (left over) by the cans?

Answer 1

`\bigtriangleup A\approx 82.41\ cm^2`

Explanation:

-Assume the cans are arranged in a two by three dimensions.

-Therefore the length of the box is equivalent to 3 diameters and the width is equivalent to two diameters:

`D=2r=2* 4=8\ cm\\\\Length=3D=3* 8=24\\\\Width=2D=2* 8=16`
`cm`

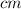
#The area of the cardboard box is calculated as:

`Area=lw\\\\=24* 16\\\\=384\ cm^2`

#The total bottom areas of the 6 cans is:

`A_6=6\pi r^2\\\\=6\pi * 4^2\\\\=301.593\ cm^2`

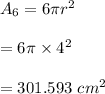
#The area not covered is the difference between the area of the box and the total bottom areas of the 6 cans:

`\bigtriangleup A=A_b-A_c\\\\=384-301.593\\\\=82.407\ cm^2\\\\\approx 82.41\ cm^2`

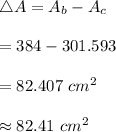
Hence, the area not covered is approximately
`82.41\ cm^2`

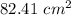
*Note that whichever order of arrangement the cans assume, the areas of the boxes will be the same.