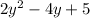Answer:
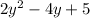
Explanation:
The complete exercise is: "What algebraic expression must be subtracted from the sum of
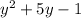 and
and
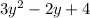 to give
to give
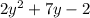 as the result?"
as the result?"
For this exercise it is necessary to remember that a sum is the result of an addition. Then, if you need to find the sum of
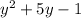 and
and
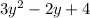 , you need to add them by combining the like terms.
, you need to add them by combining the like terms.
You also need to remember the multiplication of signs:
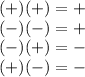
So, you get that the sum of those expression is the following:

Since you must find the algebraic expression asked in the exercise, you need to subtract the expression
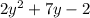 from that sum calculated above.
from that sum calculated above.
Therefore, you get:

Then, the algebraic expression asked is: