The width of the walkway is 3 feet, If the area of the garden is 484
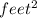 and the area covered by both the garden and the walkway (the entire square) is 784
and the area covered by both the garden and the walkway (the entire square) is 784
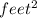 .
.
Explanation:
The given is,
Area of the garden is 484
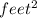
Area covered by both the garden and the walkway (the entire square) is 784
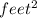 .
.
Let, x - Width of the walkway
Step:1
Formula to calculate area of square is,
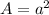 ...........................(1)
...........................(1)
Where, r - Radius of square
Step:2
For garden,
A = 484
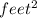
Equation (1) becomes,
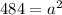
Take square root on both sides,
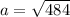
a = 22 feet
For garden and the walkway (the entire square),
A = 784
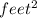
Equation (1) becomes,
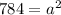
Take square root on both sides,
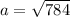
a = 28 feet
Step:3
Ref attachment,
Side of garden and the walkway =
Side of garden + 2 (width of the walkaway)....(1)
28 = 22 + 2 ( x )
2 ( x ) = 28 - 22
= 6

Width, x = 3 feet
Result:
The width of the walkway is 3 feet, If the area of the garden is 484
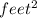 and the area covered by both the garden and the walkway (the entire square) is 784
and the area covered by both the garden and the walkway (the entire square) is 784
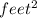 .
.