Answer:
A tangent to a circle is a straight line which touches the circle at only one point. Therefore, if
 is a tangent of
is a tangent of
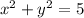 then there will be one point of intersection.
then there will be one point of intersection.
To find the point of intersection, substitute
 into
into
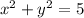 and solve for y:
and solve for y:
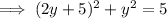

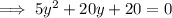
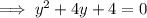
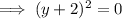
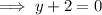
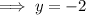
Substitute found value of y into
 and solve for x:
and solve for x:
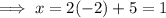
Therefore, there is one point of intersection at (1, -2), thus proving that the straight line equation is a tangent to the circle.