Question

Y=−0.04x2+0.32x+2.5

y
=
-
0
.
04
x
2
+
0
.
32
x
+
2
.
5
represents the path of an Olympic swimmer as he enters the pool. x
x
represents the distance, in feet, from the side of the pool and y
y
represents the height of the swimmer, in feet, above the pool. The side of the pool is represented by x=0

Answer 1

The swimmer enters the water about 12.86 feet from the side of the pool.

Explanation:

The correct question is

The function y=−0.04x2+0.32x+2.5 represents the path of an Olympic swimmer as he enters the pool. x represents the distance, in feet, from the side of the pool and y represents the height of the swimmer, in feet, above the pool. The side of the pool is represented by x=0

Use the quadratic formula to determine how far from the side of the pool the swimmer enters the water.

we have

`y=-0.04x^2+0.32x+2.5`

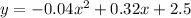
we know that

The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

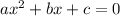
is equal to

`x=\frac{-b\pm\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`y=-0.04x^2+0.32x+2.5`

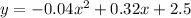
Equate the quadratic equation to zero

`-0.04x^2+0.32x+2.5=0`

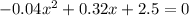
so

`a=-0.04\\b=0.32\\c=2.5`

substitute in the formula

`x=\frac{-0.32\pm\sqrt{0.32^(2)-4(-0.04)(2.5)}} {2(-0.04)}`

`x=\frac{-0.32\pm√(0.5024)} {-0.08}`

`x=\frac{-0.32+√(0.5024)} {-0.08}=-4.86`

`x=\frac{-0.32-√(0.5024)} {-0.08}=12.86`

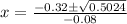
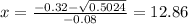
therefore

The solution is x=12.86 ft