Question

Does a triangle with side lengths 7, StartRoot 80 EndRoot, and StartRoot 31 EndRoot from a right triangle?

Use the drop-down menus to answer the following questions.

What is the square of the longest side?

What is the sum of the squares of the two shorter sides?

Is the triangle a right triangle?

Answer 1

Square of the longest side: 80

Sum of squares of two shorter sides: 80

Yes

Explanation:

7, sqrt(80) , sqrt(31)

(sqrt80)² = 7² + (sqrt31)²

80 = 49 + 31

80 = 80

Satisfies pythagoras theorem,

Hence forms a right angle triangle.

Square of the longest side: 80

Sum of squares of two shorter sides: 80

Answer 2

Answer and Step-by-step explanation:

The sides we have are 7,
`√(80)` , and
`√(31)` .

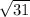The square root of 80 is less than 9 but greater than 8 (because
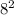`8^2` is 64,
`9^2` is 81, and 80 is in between those two values), and the square root of 31 is definitely less than the square root of 80.

So,
`√(80)` is the longest side.

1) The square of
`√(80)` is:
`(√(80) )^2=80`

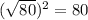
2) The sum of the squares of the two shorter sides is:

`7^2+(√(31) )^2=49+31=80`

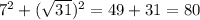
3) Since the square of the longest side is equal to the sum of the squares of the two shorter sides, by the Pythagorean Theorem, the triangle is a right triangles.

Hope this helps!