Answer:
9 quarts of paint
Explanation:
-Since, the bottom area is not painted, the total area would be the sum of the two isosceles faces and the two remaining rectangles.
#Area of Isosceles faces:
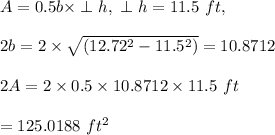
#Area of the two rectangles:
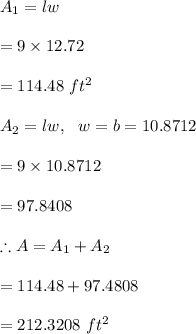
#The total area to be painted is the sum of all faces:

Since, the area would be covered twice and that 1 quart covers 80 sq ft. Let X be the number of quarts of paint:
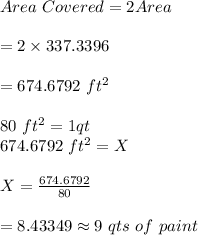
Hence, you need to buy approximately 9 quarts of paint.