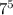Question

Simplify the expression. Assume that all variables are positive. Exponents in simplified form should all be

positive.

Answer 1

Given:

The given expression is
`\frac{7^{(1)/(2)} \cdot 7^{(3)/(2)}}{7^(-3)}`

We need to determine the exponents in simplified form.

Exponents in simplified form:

Let us determine the exponent in simplified form.

Let us apply the exponent rule
`(x^(a))/(x^(b))=x^(a-b)`

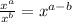
Thus, we have;

`7^{(1)/(2)+(3)/(2)-(-3)}`

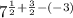
Adding the fractions, we get;

`7^{(4)/(2)-(-3)}`

Cancelling the common terms, we have;

`7^(2-(-3))`

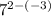
Simplifying the exponent, we get;

`7^(2+3)`

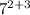
Adding the exponent, we have;

`7^5`

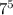
Thus, the simplified form of the expression is
`7^5`