1. Assuming
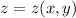 , we have
, we have
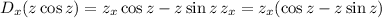
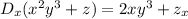
so that
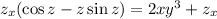
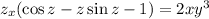
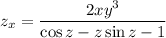
2. Let
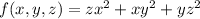 . The gradient of
. The gradient of
 is
is
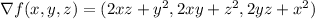
and the gradient at the desired point is
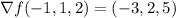
The tangent plane then has equation
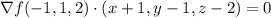


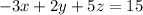
3.
 has critical points where the derivatives vanish or do not exist. The latter is irrelevant here, since
has critical points where the derivatives vanish or do not exist. The latter is irrelevant here, since
 is a polynomial and is thus continuous everywhere. So just differentiate and set the derivative equal to 0:
is a polynomial and is thus continuous everywhere. So just differentiate and set the derivative equal to 0:
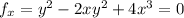
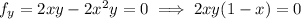
The last equation tells us
 ,
,
 , or
, or
 .
.
If
 , then in the first equation we get
, then in the first equation we get
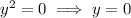 .
.
If
 , then
, then
 .
.
If
 , then
, then
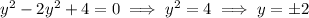 .
.
So there are 3 critical points at (0, 0), (1, -2), and (1, 2).
4. Stationary points are critical points where the derivative vanishes. So same process as in (3):

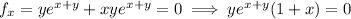
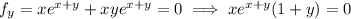
The first equation tells us
 or
or
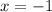 .
.
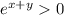 for all
for all
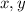 , so we can ignore this term.
, so we can ignore this term.
If
 , then
, then
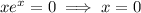 .
.
If
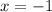 , then
, then
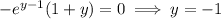 .
.
The second equation tells us
 or
or
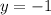 . But this gives the same information as before.
. But this gives the same information as before.
So there are only two stationary points, (0, 0) and (-1, -1).
5. First find the stationary points:
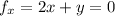
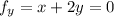
Solve this to find the one point at (0, 0). At this point, we have
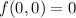 .
.
Now check for extrema along the boundary. The rectangle is bounded by the lines
 ,
,
 ,
,
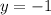 , and
, and
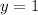 .
.
On
 , we have
, we have

which attains a minimum of 3 when
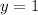 and a maximum of 7 when
and a maximum of 7 when
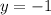 .
.
On
 , we have
, we have

which has a minimum of 3 at
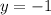 and a maximum of 7 at
and a maximum of 7 at
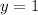
We can check on the other 2 lines, but we'd get the same information.
So we've found that
 has an absolute minimum of 0 at (0, 0), and an absolute maximum of 7 at both (-2, -1) and (2, 1).
has an absolute minimum of 0 at (0, 0), and an absolute maximum of 7 at both (-2, -1) and (2, 1).