Question

A culture started with 5000 becteria. after 2 hours it grew to 6500 becteria. Predict how many bacteria will be present after 18 hours. Round your answer to the nearest whole number. p=ae^kt

Answer 1

About 53022 bacteria present.

Explanation:

We can use the continuous growth formula:

`\displaystyle P = A e^(kt)`

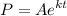
Where k is some constant.

With an initial population of 5000, it grew to 6500 after two hours.

In other words, P = 6500 when A = 5000 and t = 2:

`\displaystyle (6500) = (5000)e^(k(2))`

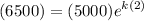
Solve for k:

`\displaystyle \begin{aligned} 6500 & = 5000e^(2k) \\ \\ e^(2k) & = (6500)/(5000) = (13)/(10) \\ \\ \ln\left(e^(2k)\right) & = \ln\left((13)/(10)\right) \\ \\ 2k & = \ln(13)/(10) \\ \\ k & = (1)/(2)\ln(13)/(10)\end{aligned}`

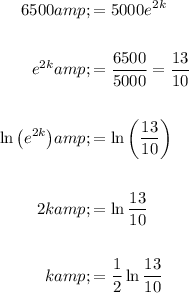
Therefore, our equation is:

`\displaystyle P = \bigg{5000e}^{(1)/(2)\ln(13)/(10)t`

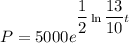
After 18 hours, t = 18. Hence:

`\displaystyle \begin{aligned} P(18) & = \bigg{5000e}^{(1)/(2)\ln(13)/(10)(18)} \\ \\ & \approx 53022\end{aligned}`

Therefore, after 18 hours, there will be about 53022 bacteria present.