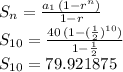Question

Evaluate each finite series for the specified number of terms...

40+20+10+...; n=10

(Please show work)

Answer 1

the sum of the first 10 terms is: 79.921875

Explanation:

Notice that this is a geometric series, of the sequence that has "40" as the first term, and the following ones are obtained by multiplying by the common ratio "1/2".

So the common ratio
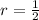`r=(1)/(2)`, and the first term
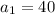`a_1=40`, then, recalling the formula for the partial sum of n terms of a geometric sequence:

`S_n=(a_1\,(1-r^n))/(1-r)`

we can find the sum of this sequence's first 10 terms (n=10):

`S_n=(a_1\,(1-r^n))/(1-r) \\S_(10)=(40\,(1-((1)/(2)) ^(10)))/(1-(1)/(2) ) \\S_(10)=79.921875`