Question

In circle P diameter QS measures 30 cm.

What is the approximate length of arc QR? Round to the nearest tenth of a centimeter

a. 7.2 cm
b. 25.8 cm
c. 94.2 cm
d. 14.4 cm

PLEASE HURRY!! I HAVE LIMITED TIME!! :)

Answer 1

Given:

The diameter of the circle P is 30 cm.

The radius of the circle P is 15 cm.

The measure of ∠RPS is 125°

We need to determine the arc length of QR.

Measure of ∠QPR:

The angles QPR and RPS are linear pairs.

Thus, we have;

`\angle QPR + \angle RPS=180^(\circ)`

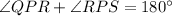
Substituting the values, we have;

`\angle QPR + 125^(\circ)=180^(\circ)`

`\angle QPR =55^(\circ)`

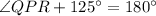
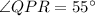
Thus, the measure of ∠QPR is 55°

Arc length of QR:

The arc length of QR can be determined using the formula,

`Arc \ length =((\theta)/(360))2 \pi r`

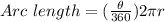
Substituting
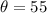`\theta=55` and r =15, we get;

`Arc \ length =((55)/(360))2 (3.14)(15)`

`Arc\ length = (5181)/(360)`

`Arc \ length =14.4 \ cm`

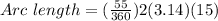
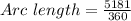
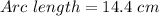
Thus, the arc length of QR is 14.4 cm.

Hence, Option d is the correct answer.