Question

How do you do this? Strugglinf

Answer 1

Formulae to use:

sin(A+B)= sinAcosB + sinBcosA

cos(A+B)=cosAcosB - sinAsinB

Consider expression
`E = \cos x+ \sin x`

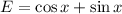
$E= \sqrt 2 (\frac{1}{\sqrt 2}\cos x + \frac{1}{\sqrt 2}\sin x)$

But we have $\sin \frac{\pi}{4}= \cos \frac{\pi}{4}=\frac{1}{\sqrt{2}}$

Thus,

$E=\sqrt{2} (\sin \frac{\pi}{4} \cos x+ \cos \frac{\pi}{4} \sin x)$

$E =\sqrt{2} (\sin (\frac{\pi}{4})+ x)$

Similarly you can simplify the denominator.

Thus we we have to simply find:

$ \frac{d}{dx} \bigg( \frac{ \sqrt{2} (\sin (\frac{\pi}{4})+ x)}{\sqrt{2} (\cos (\frac{\pi}{4})+ x)} \bigg)$

$= \frac{d}{dx} ( tan((\frac{\pi}{4}+ x))$

$= \sec ^2 (\frac{\pi}{4})+ x)$