Question

Would do anything for the answer to this question

Answer 1

Given:

The length of the entire rectangle is 10x + 7.

The width of the entire rectangle is 6x.

The length of the unshaded rectangle is 4x - 5.

The width of the unshaded rectangle is 2x.

We need to determine the area of the shaded region of the rectangle.

Area of the entire rectangle:

The area of the entire rectangle can be determined using the formula,

`A=length * width`

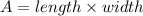
Substituting the values, we have;

`A_1=(10x+7)(6x)`

`A_1=60x^2+42x`

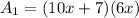
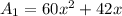
Thus, the area of the entire rectangle is 60x² + 42x

Area of the unshaded rectangle:

The area of the unshaded rectangle can be determined using the formula,

`A=length * width`

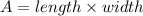
Substituting the values, we have;

`A_2=(4x-5)(2x)`

`A_2=8x^2-10x`

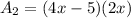
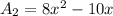
Thus, the area of the unshaded rectangle is 8x² - 10x

Area of the shaded region of the rectangle:

The area of the shaded region of the rectangle can be determined by subtracting the area of the entire rectangle by the area of the unshaded rectangle.

Thus, we have;

`A=A_1-A_2`

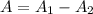
Thus, we have;

`A=60x^2+42x-(8x^2-10x)`

`A=60x^2+42x-8x^2+10x`

`A=52x^2+52x`

`A=52x(x+1)`

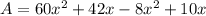
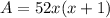
Thus, the area of the shaded region of the rectangle is 52x(x + 1)