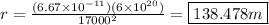Hi there!
We can begin by deriving an equation for the orbital radius.
For an object orbiting the earth, it is experiencing a centripetal force due to the force of gravitation.
Recall Newton's Law of Universal Gravitation:
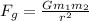
G = Gravitational Constant (6.67 × 10⁻¹¹ Nm²/kg²)
m = masses (kg)
r = radius (m)
This is equivalent to the satellite's centripetal force experienced:
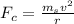
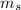 = mass of satellite (kg)
= mass of satellite (kg)
v = velocity (m/s)
r = radius (m)
Set the two equal, and rearrange for the orbital radius of the satellite.
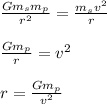
Notice that the orbital radius of the satellite does NOT depend on the satellite's mass. (we canceled it out).
Now, plug in the given values.