Question

Find the derivative.

StartFraction d Over dt EndFraction Integral from 0 to t Superscript 8 StartRoot u cubed EndRoot du
a. by evaluating the integral and differentiating the result.
b. by differentiating the integral directly.

Answer 1

Using either method, we obtain:
`t^(3)/(8)`

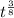
Explanation:

a) By evaluating the integral:

`(d)/(dt) \int\limits^t_0 {\sqrt[8]{u^3} } \, du`

The integral itself can be evaluated by writing the root and exponent of the variable u as:
`\sqrt[8]{u^3} =u^{(3)/(8)`

Then, an antiderivative of this is:
`(8)/(11) u^(3+8)/(8) =(8)/(11) u^(11)/(8)`

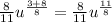
which evaluated between the limits of integration gives:

`(8)/(11) t^(11)/(8)-(8)/(11) 0^(11)/(8)=(8)/(11) t^(11)/(8)`

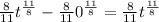
and now the derivative of this expression with respect to "t" is:

`(d)/(dt) ((8)/(11) t^(11)/(8))=(8)/(11)\,*\,(11)/(8)\,t^(3)/(8)=t^(3)/(8)`

b) by differentiating the integral directly: We use Part 1 of the Fundamental Theorem of Calculus which states:

"If f is continuous on [a,b] then

`g(x)=\int\limits^x_a {f(t)} \, dt`

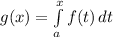
is continuous on [a,b], differentiable on (a,b) and
`g'(x)=f(x)`

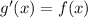
Since this this function
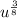`u^{(3)/(8)` is continuous starting at zero, and differentiable on values larger than zero, then we can apply the theorem. That means:

`(d)/(dt) \int\limits^t_0 {u^(3)/(8) } } \, du=t^(3)/(8)`