Given:
The given expression is
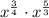
We need to simplify the given expression.
Simplification:
Let us simplify the expression using positive exponents.
Let us apply the exponent rule,
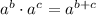
Thus, we have;
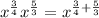
Let us simplify the exponent by taking LCM.
Thus, we get;
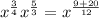
Simplifying, we get;
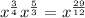
Thus, the simplified value of the given expression is
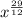
Hence, Option c is the correct answer.