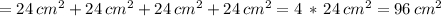Question

A regular triangular pyramid has a base and lateral faces that are congruent equilateral triangles. It has a lateral surface area of 72 square centimeters. What is the surface area of the regular triangular pyramid?

Answer 1

The total surface area of the triangular pyramid is
`96\,cm^2`

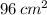
Explanation:

since the triangular pyramid has equilateral triangles as its faces, this means that all of its faces are equal, including its triangular base, because the base is a triangle that has for sides the sides of the lateral triangles (which are equilateral triangles, i.e. all sides are equal in size)

So recall that such type of pyramid has a total of 4 faces, three of them are lateral and the fourth one is the base.

The information in the problem tells us that the lateral surface of the pyramid is 72
`cm^2`, that means that the addition of its three lateral triangles renders 72
`cm^2`,

We can then find what is the area of each of the three triangles by simply dividing this number by 3 (recall that all faces in the pyramid are equal)

Each triangular face has an
`Area=(72)/(3) \,cm^2 =24\,cm^2`

Then, the total surface area of the triangular pyramid is the addition of the area of its four faces. That is:

Total surface are
`= 24\,cm^2+24\,cm^2+24\,cm^2+24\,cm^2=4\,*\,24\,cm^2=96\,cm^2`