Question

A jar of tea is placed in sunlight until it

reaches an equilibrium temperature of 31.1°C.
In an attempt to cool the liquid, which has a
mass of 177 g. 110 g of ice at 0.0°C is added.
At the time at which the temperature of the
tea is 29.1°C, find the mass of the remaining ice in the jar. The specific heat of water is 4186 J/kg.°C. Assume the specific heat capacity of the tea to be that of pure liquid water. Answer in units of g.

Answer 1

m = 4.44 [g]

Step-by-step explanation:

This is a problem related to heat transfer and thermodynamics. The second law of thermodynamics tells us that heat goes in only one direction, from the highest temperature substance to the lowest temperature. In this case the heat goes from tea to ice. The heat transfer process could be defined as the heat rejection of one body will be equal to the Heat received by another body.

`Q_(out)=Q_(in)\\Q_(out)=m*cp*(T_(f)-T_(i))`

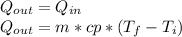
Where:

m = mass = 177[g] = 0.177[kg]

Cp = specific heat = 4186 [J/kg*C]

T_f = 29.1 [°C]

Ti = 31.1 [°C]

Q = 0.177*4186*(29.1 - 31.1)

Q = - 1481.8 [J]

Note: The negative sign means that the heat is rejected.

Recall that the heat rejected is equal to the heat transferred

As the ice is going through a phase change, the fusion latent heat should be used, i.e. when it passes from solid to liquid. The heat transfer for this process is calculated with the following expression.

Qin = m *hf

m = mass of the ice [kg]

hf = Fusion latent heat = 333700 [J/kg]

1481.8 = m * 333700

m = 0.00444 [kg] = 4.44 [g]