Question

A company has found that the daily demand x for its boxes of chocolates is inversely proportional to the price p. When the price is $5, the demand is 800 boxes. Approximate the demand when the price is increased to $6.

Answer 1

The demand is 667 boxes when the price is increased to $6.

Explanation:

Given that,

• The variable x is the demand and
• The variable p is the price.
• Let k be the constant of proportionality.

We then express the inverse relationship as:

⇒
`x = (k)/(p)`

⇒
`k=xp`

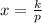
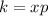
It is given that, when the price is $5, the demand is 800 boxes.

So, substitute x=800 and p=5

⇒
`k=800* 5`

⇒
`k=4000`

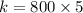
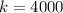
To find the price increased to $6 :

Now, substitute x = 6 and k = 4000 to solve for p.

⇒
`p=(k)/(x)\\\\`

`=(4000)/(6)\\\\`

`=666.6667`

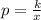
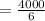
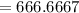
⇒ 667 (approximately)

Therefore, the demand at a price of $6 is approximately 667 boxes.