Question

A biologist is trying to determine the average age of a local forest. She cuts down 18 randomly selected trees and counts the number of tree rings, which can be used to estimate the age of the tree. What critical value should she use to construct a 99% confidence interval

Answer 1

The critical value of t for 99% confidence interval is 2.898.

Explanation:

The complete question is:

A biologist is trying to determine the average age of a local forest. She cuts down 18 randomly selected trees and counts the tree rings. They find the average number of tree rings to be 83 with a variance of 320. What is the critical value for the 99% confidence interval?

The population variance is not known and the sample size is too small. So a t-confidence interval will be used to estimate the population mean age of a local forest.

The (1 - α)% confidence interval for population mean is:

`CI=\bar x\pm t_(\alpha/2, (n-1))* (s)/(√(n))`

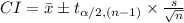
The information provided is:

n = 18

(1 - α)% = 99%

The degrees of freedom of the critical value of t is:

n - 1 = 18 - 1 = 17

Compute the critical value of t as follows:

`t_(\alpha/2, (n-1))=t_(0.01/2, (18-1))=t_(0.005, 17)=2.898`

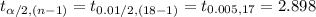
*Use a t-table.

Thus, the critical value of t for 99% confidence interval is 2.898.