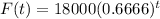Question

The fish population of a lake is decreasing each year. A study is conducted. But, unfortunately some data was lost. The researcher found in her notes that in year one the fish population was 18000 fish and in year three the fish population was 8000 fish. Assume a constant rate of decay. Find a formula F

Answer 1

`F(t) = 18000(0.6666)^(t)`

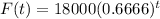
Explanation:

The fish population after t years can be modeled by the following equation:

`F(t) = F(0)(1-r)^(t)`

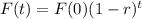
In which F(0) is the initial population and r is the constant rate of decay.

Year one the fish population was 18000

This means that
`F(0) = 18000`

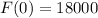
In year three the fish population was 8000 fish.

Two years later, so
`F(2) = 8000`

`F(t) = F(0)(1-r)^(t)`

`8000 = 18000(1-r)^(2)`

`(1-r)^(2) = 0.4444`

`\sqrt{(1-r)^(2)} = √(0.4444)`

`1 - r = 0.6666`

`r = 0.3334`

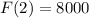
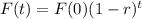
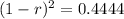
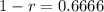
So

`F(t) = 18000(0.6666)^(t)`