Answer:
a) 0.214 or 21.4%
b) P=0.011
c) The realtor should sample at least 551 homes.
Explanation:
The current thinking is that housing prices follow an approximately normal model with mean $238,000 and standard deviation $5,041.
a) We need to know the proportion of housing prices in Athens that are less than $234,000. We can calculate this from the z-score for the population distribution.
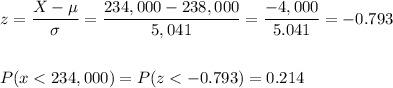
The proportion of housing prices in Athens that are less than $234,000 is 0.214.
b) Now, a sample is taken. The size of the sample is n=134.
We have to calculate the probability that the average selling price is greater than $239,000.
In this case, we have to use the standard error of the sampling distribution to calculate the z-score:
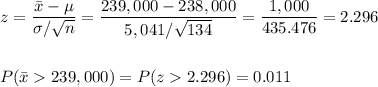
The probability that the average selling price is greater than $239,000 is 0.011.
c) We have another sample taken from a distribution with the same parameters.
We have to calculate the sample size so that the margin of error for a 98% confidence interval is $500.
The expression for the margin of error of the confidence interval is:
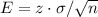
We can isolate n from the margin of error equation as:
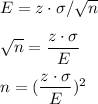
We have to look for the critical value of z for a 98% CI. This value is z=2.327.
Now we can calculate the minimum value for n to achieve the desired precision for the interval:

The realtor should sample at least 551 homes.