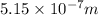Question

A Young's interference experiment is performed with blue-green laser light. The separation between the slits is 0.500 mm, and the screen is located 3.14 m from the slits. The first bright fringe is located 3.24 mm from the center of the interference pattern. What is the wavelength of the laser light?

Answer 1

Wavelength of laser light will be
`5.15* 10^(-7)m`

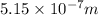
Step-by-step explanation:

We have given distance between the slits d = 0.5 mm =
`0.5* 10^(-3)m`

Distance between screen and slits D = 3.14 m

Distance of bright fringe from center
`y=3.24mm=3.24* 10^(-3)m`

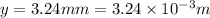
It is known that
`sin\Theta =(y)/(D)=(3.24* 10^(-3))/(3.14)=1.031* 10^(-3)m`

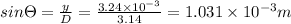
It is also know that
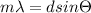`m\lambda =dsin\Theta`, here m = 1 for first bight fringe.

`1* \lambda =0.5* 10^(-3)* 1.031* 10^(-3)`

`\lambda =5.15* 10^(-7)m`

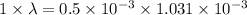
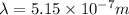
So wavelength of laser light will be
`5.15* 10^(-7)m`