Question

You have a spring that stretches 0.070 m when a 0.10-kg block is attached to and hangs from it. Imagine that you slowly pull down with a spring scale so the block is now below the equilibrium position where it was hanging at rest. The scale reading when you let go of the block is 3.0 N.

Part A
Where was the block when you let go? Assume y0 is the equilibrium position of the block and that "down" is the positive direction.

Part B
Determine the work you did stretching the spring.
Express your answer to two significant figures and include the appropriate units.

Part C
What was the energy of the spring-Earth system when you let go (assume that zero potential energy corresponds to the equilibrium position of the block)?
Express your answer to two significant figures and include the appropriate units.

Part D
How far will the block rise after you release it?
Express your answer to two significant figures and include the appropriate units.

Answer 1

a) x = 0.144 m

b) W = 0.15 J

c) E = 0.14 J

d) The block will rise 0.07m after it is released

Step-by-step explanation:

a) The elastic force equals the gravitational force

F = kx = mg

x = 0.07, m = 0.1 kg, g = 9.81 m/s²

0.07k = 0.1 * 9.8

k = (0.1*9.8)/0.07

k = 14 N/m

When the force, F = 3N

F = kx

3 = 14x

x = 3/14

x = 0.214 m

The position of the block = 0.214 - 0.07 = 0.144m

B) Determine the work you did stretching the spring.

Energy stored in the spring when x = 0.07

E = 0.5 kx²

E = 0.5 * 14 * 0.07²

E = 0.0343 J

Energy stored in the spring when x = 0.214

E = 0.5 kx²

E = 0.5 * 14 * 0.214²

E = 0.32 J

Potential energy lost due to gravity = mgh

PE = 0.1 * 9.81 * 0.144

PE = 0.141 J

So to calculate the work done:

0.0343 + W = 0.32 - 0.141

W = 0.15 J

c) Energy in the spring

E = 0.32 - 0.0343 - 0.15

E = 0.1357 = 0.14 J

d)

`1/2 *k *0.214^(2) = 1/2 kx^(2) + mg(0.214+x)\\0.32 = 7x^(2) + 0.1*9.8(0.214+x)\\`

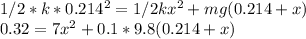
Solving for x, x = 0.07 m

The block will rise 0.07m after it is released