Question

(5) In the center of the monument are two concentric circles of igneous rock pillars, called bluestones. The construction of these circles was never completed. These circles are known as the Bluestone Circle and the Bluestone Horseshoe. The stones in these two formations were transported to the site from the Prescelly Mountains in Pembrokeshire, southwest Wales. Excavation at the center of the monument revealed an antler, an antler tine, and an animal bone. Each artifact was submitted for dating. It was determined that this sample of three artifacts had a mean age of 2193.3 BCE, with a standard deviation of 104.1 years. Assume that the ages are normally distributed with no obvious outliers. Use an α = 0.05 significance level to test the claim that the population mean age of the Bluestone formations is different from Corbin's declared mean age of the ditch, that is, 2950 BCE.

Answer 1

There is enough evidence, at a significance level of 0.05, that the population mean age of the Bluestone formations is different from 2950 BCE.

Explanation:

We have a sample and we want to perform a hypothesis test on the mean.

The null hypothesis is the Corbin's declared age (2950 BCE). The alternative hypothesis states that the age differ from that value.

They can be expressed as:

`\H_0:\mu=2950\\\\H_a:\mu\\eq2950`

The significance level is 0.05.

The sample has a size of n=3, a mean of 2193.3 BCE and a standard deviation of 104.1 years.

As the standard deviation is estimated from the sample, we have to calculate the t-statistic.

`t=(\bar x-\mu)/(s/√(n))=(2193.3-2950)/(104.1/√(3))=(-756.7)/(60.1)=-12.59`

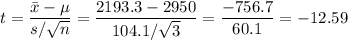
The degrees of freedom for this test are:

`df=n-1=3-1=2`

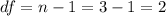
The critical value for a two side test with level of significance α=0.05 and 2 degrees of freedom is t=±4.271.

As the statistic t=-12.59 lies outside of the acceptance region, the null hypothesis is rejected.

There is enough evidence, at a significance level of 0.05, that the population mean age of the Bluestone formations is different from 2950 BCE.