Answer:
1) 883 kgm2
2) 532 kgm2
3) 2.99 rad/s
4) 944 J
5) 6.87 m/s2
6) 1.8 rad/s
Step-by-step explanation:
1)Suppose the spinning platform disk is solid with a uniform distributed mass. Then its moments of inertia is:

If we treat the person as a point mass, then the total moment of inertia of the system about the center of the disk when the person stands on the rim of the disk:
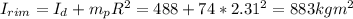
2) Similarly, he total moment of inertia of the system about the center of the disk when the person stands at the final location 2/3 of the way toward the center of the disk (1/3 of the radius from the center):
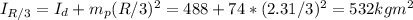
3) Since there's no external force, we can apply the law of momentum conservation to calculate the angular velocity at R/3 from the center:
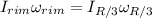
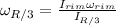
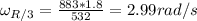
4)Kinetic energy before:
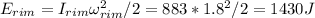
Kinetic energy after:
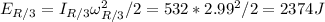
So the change in kinetic energy is: 2374 - 1430 = 944 J
5)
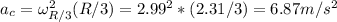
6) If the person now walks back to the rim of the disk, then his final angular speed would be back to the original, which is 1.8 rad/s due to conservation of angular momentum.