Question

Flying against the wind, an airplane travels 4560 kilometers in 6 hours. Flying with the wind, the same plane travels 3720 kilometers in 3 hours. What is the rate of the plane in still air and what is the rate of the wind?

Answer 1

The speed rate of the plane in still air is 1006.67 km/h

The speed rate of the wind is 246.67 km/h

Explanation:

To answer the question, we let the speed of the plane in still air = x km/h

Let the speed of the wind = y km/h

Therefore,

4560/(x - y) = 6 hours and

3720/(x + y) = 3 hours

4560 = 6·x - 6·y.........(1)

3720 = 3·x + 3·y ........(2)

Multiplying equation (2) by 2 and add to (1) gives

12080 = 12·x

x = 12080/12 =
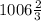`1006(2)/(3)` km/h

Substituting the value of x in (1) gives

4560 = 6040 - 6·y

6·y = 1480

y = 1480/6 =
`246(2)/(3)`

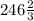
The speed rate of the plane in still air = 1006.67 km/h

The speed rate of the wind = 246.67 km/h.