Question

According to a report in USAToday, more and more parents are helping their young adult children get homes. Suppose eight persons in a random sample of 40 young adults who recently purchased a home in Kentucky received help from their parents. You have been asked to construct a 95% confidence interval for the population proportion of all young adults in Kentucky who received help from their parents. What is the margin of error for a 95% confidence interval for the population proportion?

Answer 1

a) 95% confidence interval for the population proportion of all young adults in Kentucky who received help from their parents.

( 0.0761 , 0.3239)

b) Margin of error = 0.1264.

Explanation:

Explanation:-

Given '8' persons in a random sample of 40 young adults who recently purchased a home in Kentucky received help from their parents.

sample proportion of success
`'p' = (8)/(40) = 0.2`

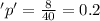
q = 1=p

q = 1-0.2 = 0.8

a)

95% confidence interval for the population proportion of all young adults in Kentucky who received help from their parents.

`(p-1.96\sqrt{(pq)/(n) } , p+1.96\sqrt{(pq)/(n) } )`

`(0.2-1.96\sqrt{(0.2X0.8)/(40) } , 0.2+1.96\sqrt{(0.2X0.8)/(40) } )`

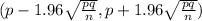
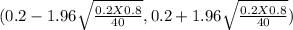
(0.2 - 0.1239,0.2+0.1239)

( 0.0761 , 0.3239)

b) the margin of error for a 95% confidence interval for the population proportion.

For the 95% confidence interval ∝= 0.05 and zₐ = 1.96≅2.

`Margin of error = (2√(pq) )/(√(n) )`

`Margin of error = (2√(0.2X0.8) )/(√(40) )`

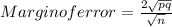
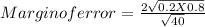
Margin of error for a 95% confidence interval for the population proportion.

Margin of error = 0.1264.