Question

Select the equivalent expression

Answer 1

The equivalent expression is: (C)
`$(1)/(3^9 \cdot 6^(18))$`.

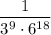To simplify the given expression, we can apply the rules of exponents.

First, we raise 3 to the power of 3 and 6 to the power of 6, individually:

3^3 = 27 and 6^6 = 46656.

Next, we multiply these two values together:

27 * 46656 = 1259712.

Now, we raise the result to the power of -3:

1259712^(-3).

To simplify this expression, we can rewrite it as the reciprocal of the base raised to the positive exponent:

(1 / 1259712^3).

This can be further simplified by raising the base to the power of 3:

(1 / (1259712 * 1259712 * 1259712)).

Finally, we can simplify the expression by multiplying the denominators:

1 / (1954890816015872).

Answer 2

Given:

The given expression is
`\left(3^(3) \cdot 6^(6)\right)^(-3)`

We need to determine the equivalent expression.

Equivalent expression:

The equivalent expression can be determined by solving the given expression.

Let us apply the exponent rule,
`a^(-b)=(1)/(a^(b))`

Thus, we get;

`(1)/(\left(3^(3) \cdot 6^(6)\right)^(3))`

Again, applying the exponent rule,
`(a \cdot b)^(n)=a^(n) b^(n)`

Thus, we have;

`(1)/(\left(3^(3))^3 \cdot (6^(6)\right)^(3))`

Simplifying, we get;

`(1)/(3^(9) \cdot 6^(18))`

Thus, the equivalent expression is
`(1)/(3^(9) \cdot 6^(18))`

Hence, Option C is the correct answer.