Answer:
32.55 cm
Explanation:
Let x = the length of wire that becomes a circle.
Then 74 - x = the length of wire that becomes a square
Circumference of circle + perimeter of square = 74
1. Expression for the side of the square
P = 4s = 74 - x
s = ¼(74 - x)
2. Expression for the radius of the circle
C = 2πr = x
r = x/(2π)
3. Expression for the total area
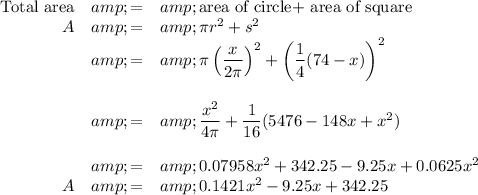
This is the equation of a parabola.
In standard form,
ƒ(x) = 0.1421x² -9.25x + 342.24
a = 0.1421; b = -9.25; c = 342.24
The parabola opens upwards, because a > 0. Therefore, the vertex is a minimum.
The vertex of a parabola occurs at
x = -b/(2a) = 9.25/(2 × 0.1421) = 9.25/(0.2842) = 32.55
The circumference of the circle is 32.55 cm.
The graph below shows that the area of the circle is a minimum when x = 32.55 cm