Question

In ΔTUV, the measure of ∠V=90°, the measure of ∠T=16°, and VT = 4.9 feet. Find the length of TU to the nearest tenth of a foot.

Answer 1

Given:

Given that TUV is a right triangle.

The measure of ∠T is 16°

The length of VT is 4.9 feet.

We need to determine the length of TU.

Length of TU:

The length of TU can be determined using the trigonometric ratio.

Thus, we have;

`cos \ \theta=(adj)/(hyp)`

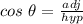
where
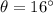`\theta=16^(\circ)`, adj = TV and hyp = TU

Thus, we get;

`cos \ 16^(\circ)=(4.9)/(TU)`

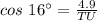
Simplifying, we get;

`TU=(4.9)/(cos \ 16^(\circ))`

`TU=(4.9)/(0.9613)`

`TU=5.097`

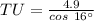
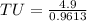
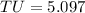
Rounding off to the nearest tenth, we get;

`TU=5.1`

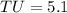
Thus, the length of TU is 5.1 feet.