Question

A 20 kg box on a horizontal frictionless surface is moving to the right at a speed of 4.0 m/s. The box hits and remains attached to one end of a spring of negligible mass whose other end is attached to a wall. As a result, the spring compresses a maximum distance of 0.50 m, and the box then oscillates back and forth. (a) i. The spring does work on the box from the moment the box first hits the spring to the moment the spring first reaches its maximum compression. Indicate whether the work done by the spring is positive, negative, or zero. ____ Positive ____ Negative ____ Zero Justify your answer. ii. Calculate the magnitude of the work described in part i. (b) Calculate the spring constant of the spring. (c) Calculate the magnitude of the maximum acceleration of the box. (d) Calculate the frequency of the oscillation of the box. (e) Let x

Answer 1

a)

i) Negative

ii) 160 J

b) 1280 N/m

c)
`32 m/s^2`

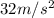
d) 1.27 Hz

e)

i) See attached plot

ii) See attached plot

Step-by-step explanation:

a)

i) The work done by a force is given by

`W=Fx cos \theta`

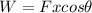
where

F is the force

x is the displacement of the object

`\theta` is the angle between the direction of the force and the direction

Here we have:

- The force that the spring exerts on the box is to the left (because the box is moving to the right, trying to compress the spring)

- The displacement of the box is to the right

So, F and x have opposite direction, and so
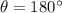`\theta=180^(\circ)` and
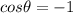`cos \theta=-1`, which means that the work done is negative.

ii)

According to the work-energy theorem, the work done by the spring is equal to the change in kinetic energy of the box:

`W=K_f - K_i = (1)/(2)mv^2-(1)/(2)mu^2`

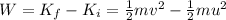
where

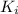`K_i` is the initial kinetic energy of the box

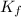`K_f` is the final kinetic energy

m = 20 kg is the mass of the box

u = 4.0 m/s is its initial speed

v = 0 m/s is the final speed (the box comes to rest)

Therefore,

`W=(1)/(2)(20)(0)^2-(1)/(2)(20)(4.0)^2=-160 J`

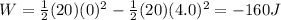
So, the magnitude is 160 J.

b)

The elastic energy stored in a spring when it is compressed is given by

`U=(1)/(2)kx^2`

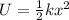
where

k is the spring constant

x is the stretching/compression of the spring

Due to the law of conservation of energy, the kinetic energy lost by the box is equal to the elastic energy gained by the spring, so:

`|W|=U=(1)/(2)kx^2`

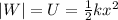
We have

`|W|=160 J`

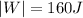
x = 0.50 m is the maximum compression of the spring

Solving for k:

`k=(2U)/(x^2)=(2(160))/((0.50)^2)=1280 N/m`

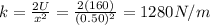
c)

The magnitude of the force exerted on the box is given by

`F=kx`

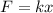
where

k = 1280 N/m is the spring constant

x = 0.50 m is the compression of the spring

Substituting,

`F=(1280)(0.50)=640 N`

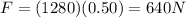
Now we can find the maxmum acceleration using Newton's second law:

`a=(F)/(m)`

where

F = 640 N is the maximum force

m = 20 kg is the mass of the box

So,

`a=(640)/(20)=32 m/s^2`

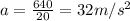
d)

The frequency of oscillation of a spring-mass system is given by

`f=(1)/(2\pi)\sqrt{(k)/(m)}`

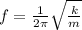
where

k is the spring constant

m is the mass

Here we have:

k = 1280 N/m is the spring constant of this spring

m = 20 kg is the mass of the box

So, the frequency of this system is:

`f=(1)/(2\pi)\sqrt{(1280)/(20)}=1.27 Hz`

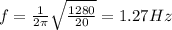
e)

i)

Here we want to sketch the kinetic energy of the box as a function of the position, x: find this graph in attachment.

In a spring-mass oscillating system, the kinetic energy is zero when the system is at the extreme position, i.e. when the spring is maximum compressed/stretched. In this problem, this happens when x = - 0.50 m and x = +0.50 m (we called x = 0 the position of equilibrium of the spring). In these positions in fact, the mass has zero speed, so its kinetic energy is zero.

On the other hand, the box has maximum speed when x = 0 (because it's the moment where all the elastic energy is converted into kinetic energy, which is therefore maximum, and so the speed is also maximum).

ii)

Here we want to plot the acceleration of the box as a function of the position x: find the graph in attachment.

In a spring-mass system, the acceleration is proportional to the negative of the displacement, since the restoring force

`F=-kx`

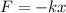
By rewriting the force using Newton's second Law, we have

`ma=-kx \\a=-(k)/(m)x`

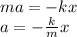
Which means that acceleration is proportional to the displacement, but with opposite sign: so, this graph is a straight line with negative slope.