Question

Determine the perimeter of AGN .

Answer 1

150

Explanation:

Segment AE divides the triangle into two congruent right angle triangles

AG = AN = 35 + 21 = 56

NG = 2(19) = 38

Perimeter = 56 + 56 + 38

150

Answer 2

Given:

Given that AGN is a triangle with circle inscribed in it.

The circle touch the triangle at the point R, T and E.

The length of AR is 35 units.

The length of RG is 21 units.

The length of NE is 19 units.

We need to determine the perimeter of the triangle AGN.

Length of GE:

Since, we know the property that, "if two segments from a exterior point are tangent to the circle, then they are congruent".

Since, RG and EG from an exterior point G are tangents to the circle, then RG and EG are congruent.

Thus, we have;

`RG=EG`

`21=EG`

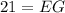
Thus, the length of GE is 21 units.

Length of TN:

Since, we know the property that, "if two segments from a exterior point are tangent to the circle, then they are congruent".

Since, TN and NE from an exterior point N are tangents to the circle, then TN and NE are congruent.

Thus, we have;

`TN=NE`

`TN=19`

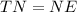
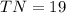
Thus, the length of TN is 19 units.

Length of AT:

Since, we know the property that, "if two segments from a exterior point are tangent to the circle, then they are congruent".

Since, AT and AR from an exterior point A are tangents to the circle, then AT and AR are congruent.

Thus, we have;

`AT=AR`

`AT=35`

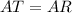
Thus, the length of AT is 35 units.

Perimeter of AGN:

The perimeter of AGN is given by

`\triangle AGN=AR+RG+GE+EN+TN+AT`

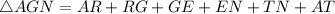
Substituting the values, we get;

`\triangle AGN=35+21+21+19+19+35`

`\triangle AGN=150`

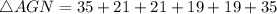
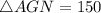
Thus, the perimeter of the triangle AGN is 150 units.