Given:
The radius of the circle is 12 units.
The central angle of the shaded region is 90°
We need to determine the arc length of the shaded region.
Arc length:
The arc length of the shaded region can be determined using the formula,
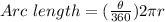
substituting
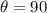 and r = 12, we get;
and r = 12, we get;
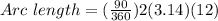
Multiplying the terms, we have;
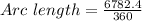
Dividing, we get;

Rounding off to the nearest tenth, we get;
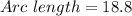
Thus, the arc length of the shaded region is 18.8 units.