Given:
Given that the radius of the hemisphere is 9.8 inches.
We need to determine the volume of the hemisphere.
Volume of the hemisphere:
The volume of the hemisphere can be determined using the formula,
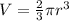
where r is the radius of the hemisphere.
Substituting r = 9.8 in the above formula, we get;
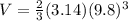
Simplifying, we get;
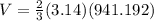
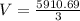
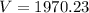
Rounding off to the nearest tenth, we get;

Thus, the volume of the hemisphere is 1970.2 cubic inches.