Question

Derive an algebraic equation for the vertical force that the bench exerts on the book at the lowest point of the circular path in terms of the book’s mass mb , tangential speed vb , radius R of the path, and physical constants, as appropriate. Do not substitute any numerical values for variables or physical constants.

Answer 1

a)

i) 120 s

ii) 1.57 m/s

b)

i) See attachment

ii) Up

c)
`N=mg+m(v_b^2)/(R)`

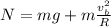
d) Greater than

Step-by-step explanation:

The problem is incomplete: find the complete text in attachments.

a)

i) The period of revolution of the book is equal to the total time taken by the book to complete one revolution.

Looking at the graph, the period of revolution can be estimated by evaluating the difference in time between two consecutive points of the motion of the book that have the same shape.

For instance, we can evaluate the period by calculating the difference in time between two consecutive crests. We see that:

- The first crest occur at t = 90 s

- The second crest occurs at t = 210 s

Therefore, the period of revolution is

T = 210 - 90 = 120 s

ii)

The tangential speed of the book is given by the ratio between the distance covered during one revolution (so, the perimeter of the wheel) and the period of revolution.

Mathematically:

`v_b=(2\pi R)/(T)`

where

R is the radius of the wheel

T = 120 s is the period

From the graph, we see that the maximum position of the book is x = +30 m, while the minimum position is x = -30 m, so the diameter of the wheel is

d = +30 - (-30) = 60 m

So the radius is

R = d/2 = 30 m

So, the speed is

`v_b=(2\pi (30))/(120)=1.57 m/s`

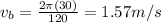
b)

i) See in attachment the free-body diagram of the book at its lowest position.

There are 2 forces acting on the book at the lowest position:

- The weight of the book, of magnitude

`W=mg`

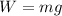
where m is the mass of the book and g the acceleration due to gravity. This force acts downward

- The normal force exerted by the bench on the book, of magnitude N. This force acts upward

ii)

When the book is at its lowest position, it is moving horizontally at constant speed.

However, the book is accelerating. In fact, acceleration is the rate of change of velocity, and velocity is a vector, so it has both a speed and a direction; here the speed is not changing, however, the direction is changing (upward), so the book has an upward net acceleration.

According to Newton's second law of motion, the net vertical force on the book is proportional to its net vertical acceleration:

`F=ma`

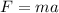
where F is the net force, m is the mass, a is the acceleration. Therefore, since a is different from zero, the book has a net vertical force, in the same direction of the acceleration (so, upward).

c)

As we said in part b), there are two forces acting on the book at its lowest position:

- The weight,
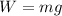`W=mg`, downward

- The normal force of the bench, N, upward

Since the book is in uniform circular motion, the net force on it must be equal to the centripetal force
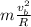`m(v_b^2)/(R)`, so we can write:

`N-mg=m(v_b^2)/(R)`

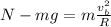
where

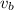`v_b` is the speed of the book

R is the radius of the path

Therefore, we find an expression for the normal force:

`N=mg+m(v_b^2)/(R)`

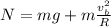
d)

As we said in part c) and d):

- The normal force acting on the book at its lowest position is

`N=mg+m(v_b^2)/(R)`

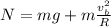
- The weight (force of gravity) of the book is

`W=mg`

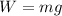
By comparing the two equations above, we observe that

`N>W`

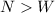
Therefore, we can conclude that the normal force exerted by the bench on the book is greater than the weight of the book.