Question

Calculate the mass of KOH in a 35% solution that contains 58.5 g of water.

Answer 1

Approximately
`\rm 31.5\; g`.

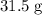Step-by-step explanation:

The mass of a solution can be divided into two parts:

• the solute (the material that was dissolved,) and
• the solvent.

In this particular
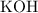`\rm KOH` solution in water,

• 
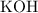  `\rm KOH` is the solute, while
• water is the solvent.

The number
`35\%` here likely refers to the concentration of
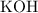`\rm KOH` in this solution. That's ratio between the mass of the solute (
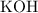`\rm KOH`) and the mass of the whole solution (mass of solute plus mass of solvent.) That is:

`\displaystyle \frac{m(\text{KOH})}{m(\text{solution})} = 35\% = 0.35`.

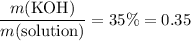Hence,
`m(\mathrm{KOH}) = 0.35\, m(\text{solution})`.

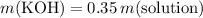However, since the solution contains only the solute and the solvent,
`m(\text{solution}) = m(\text{solute}) + m(\text{solvent})`.

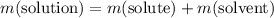For this solution in particular,

`\begin{aligned}&m(\text{solution})\\&= m(\text{solute}) + m(\text{solvent}) \\ &= m(\text{KOH}) + m(\text{water})\end{aligned}`.

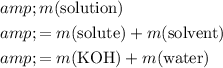As a result,

`\begin{aligned}&m(\mathrm{KOH})\\ &= 0.35\, m(\text{solution}) \\&= 0.35\, (m(\mathrm{KOH}) + m(\text{water}))\\&= 0.35\, m(\mathrm{KOH}) + 0.35 \, m(\text{water})\end{aligned}`.

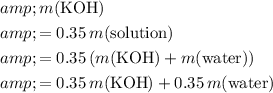Subtract
`0.35\, m(\mathrm{KOH})` from both sides of the equation:

`(1 - 0.35)\, m(\mathrm{KOH}) = 0.35\, m(\text{water})`.

`\begin{aligned} &m(\mathrm{KOH}) \\ &= \left((0.35)/(1 - 0.35)\right)\cdot m(\text{water}) \\ &= (0.35)/(0.65) * 58.5\; \text{g} = 31.5 \; \text{g}\end{aligned}`.

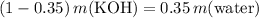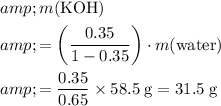Note, that for this calculation, there's nothing special about this
`35\%` solution of
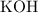`\mathrm{KOH}` in water. In general,

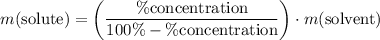`\displaystyle m(\text{solute}) = \left(\frac{\%\text{concentration}}{100\% - \%\text{concentration}}\right)\cdot m(\text{solvent})`.