Question

A flexible container at an initial volume of 8.15 L contains 7.51 mol of a gas. More gas is

then added to the container until it reaches a final volume of 13.9 L. Assuming the
pressure and the temperature of the gas remained constant, calculate the moles of gas
added to the container.
15.1 mol
O 5.5 mol
0 4.40 mol
12.8 mol

Answer 1

The answer for the following problem is mentioned below.

• Therefore the final moles of the gas is 12.8 moles
• Therefore the option is "D" (12.8 moles)

Step-by-step explanation:

Given:

Initial moles (
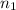`n_(1)`) = 7.51 moles

Initial volume (
`V_(1)`) = 8.15 L

Final volume (
`V_(2)`) = 13.9 L

To find:

Final moles of the gas

We know;

From the ideal gas equation;

P × V = n × R × T

where;

P represents the pressure of the gas

V represents the volume of the gas

n represents the no of moles of the gas

R represents the universal gas constant

T represents the temperature of the gas

we know;

from the above mentioned equation,

V ∝ n

So,

`(V_(1) )/(V_(2) )` =
`(n_(1) )/(n_(2) )`

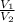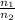
where,

`V_(1)` represents the initial volume

`V_(2)` represents the final volume

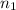`n_(1)` represents the initial moles

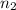`n_(2)` represents the final moles

So,

`(8.15)/(13.9)` =
`(7.51)/(n_(2) )`

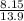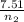
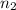`n_(2)` = 12.8 moles

Therefore the final moles of the gas is 12.8 moles